如何理解标量、向量和张量？零维到三维的演变可视化

我们相信：世界是美好的，你是我也是。 来玩一下解压小游戏吧！

在机器学习领域，一直存在着标量、向量（矢量）和张量的说法，那么，两者到底有甚么区别呢？苏南大叔在本文中，将要通过Python和 Matplotlib的可视化工具，直观地展示了标量、向量和张量的区别及其表示方式。

苏南大叔的“程序如此灵动”博客，记录苏南大叔的代码编程经验总结。测试环境：win10，python@3.12.9，pip@25.0.1，matplotlib@3.10.1。著名的机器学习框架tensorflow中的tensor就指的是张量。

基本概念

张量是机器学习中用来存储数据的“多维容器”，可以简单理解为升级版的数组，不同维度的张量可以装不同复杂程度的数据。

标量、向量和张量的区别：

• 0维张量（标量）：一个单独的数字，比如重量（例如10斤）。
• 1维张量（向量）：一列数字（数组）表示大小和方向，比如销售员每月的销量（例如 [10, 30, 50]）。
• 2维张量（矩阵）：表格数据，比如销量表（行是每月销量，列是产品）。
• 3维及以上张量：更高维数据，比如彩图（宽、高、颜色通道）、视频（时间、宽、高、颜色通道）。

所以，张量的范围很广，它是一个广义的说法。包括了标量、向量、矩阵等等说法。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 设置字体以支持中文
rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
rcParams['axes.unicode_minus'] = False   # 解决负号显示问题

标量 (Scalar) 零维

• 标量是一个零维的数值，表示单一的量。
• 例如：18 是一个标量。

# 标量：零维数组
scalar = np.array(18)
print("标量 (Scalar):")
print(scalar)
print("维度 (Shape):", scalar.shape)  # 输出 ()

# 绘制标量
fig1 = plt.figure(figsize=(4, 4))
ax1 = fig1.add_subplot(111)
ax1.text(0.5, 0.5, str(scalar), fontsize=20, ha='center', va='center')
ax1.set_title("标量 (Scalar)")
ax1.axis('off')
plt.show()

图中显示了一个单独的值 18，表示标量。

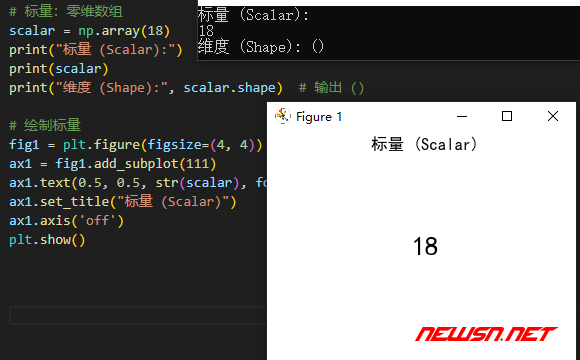
向量 (Vector) 一维数组

• 向量是一维数组，表示具有大小和方向的量。
• 例如：[1, 2, 3] 是一个向量。

# 向量：一维数组
vector = np.array([1, 2, 3])
print("\n向量 (Vector):")
print(vector)
print("维度 (Shape):", vector.shape)  # 输出 (3,)

# 绘制向量
fig2 = plt.figure(figsize=(6, 4))
ax2 = fig2.add_subplot(111)
ax2.plot(vector, marker='o')
ax2.set_title("向量 (Vector)")
ax2.set_xticks(range(len(vector)))
ax2.set_xlabel("索引 (Index)")
ax2.set_ylabel("值 (Value)")
plt.show()

这里绘制了一维数组 [1, 2, 3] 的折线图，展示了向量的大小和方向。

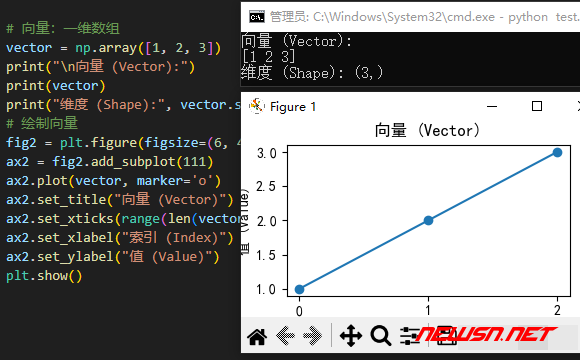
张量 (Tensor) 二维三维矩阵及更多

• 张量是更高维度的数组，可以是二维（矩阵）、三维（矩阵）或更高维度。

• 例如：

  • 二维张量（矩阵）：[[1, 2, 3], [4, 5, 6]]
  • 三维张量：[[[1, 2], [3, 4]], [[5, 6], [7, 8]]]

# 张量：二维数组（矩阵）
tensor_2d = np.array([[1, 2, 3], [4, 5, 6]])
print("\n二维张量 (2D Tensor):")
print(tensor_2d)
print("维度 (Shape):", tensor_2d.shape)  # 输出 (2, 3)

# 绘制二维张量
fig3 = plt.figure(figsize=(6, 4))
ax3 = fig3.add_subplot(111)
ax3.imshow(tensor_2d, cmap='Blues', interpolation='none')
ax3.set_title("二维张量 (2D Tensor)")
ax3.set_xticks(range(tensor_2d.shape[1]))
ax3.set_yticks(range(tensor_2d.shape[0]))
ax3.set_xlabel("列 (Columns)")
ax3.set_ylabel("行 (Rows)")
plt.show()

使用 imshow 显示了二维数组（矩阵）[[1, 2, 3], [4, 5, 6]]，以颜色块的形式表示矩阵的值。

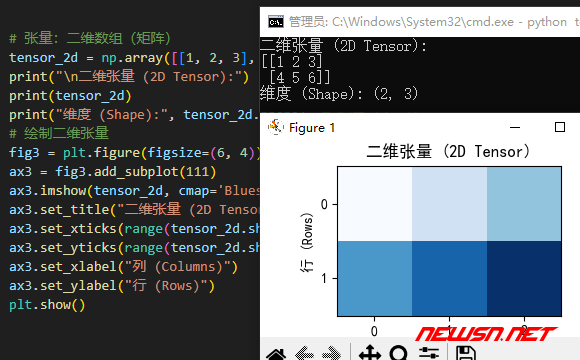
# 张量：三维数组
tensor_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print("\n三维张量 (3D Tensor):")
print(tensor_3d)
print("维度 (Shape):", tensor_3d.shape)  # 输出 (2, 2, 2)

# 绘制三维张量
fig4 = plt.figure(figsize=(8, 6))
ax4 = fig4.add_subplot(111, projection='3d')
x, y, z = np.indices((3, 3, 3))  # 修改为 (3, 3, 3)
filled = np.zeros((3, 3, 3), dtype=bool)  # 初始化为全 False
filled[:2, :2, :2] = True  # 只填充 (2, 2, 2) 的区域
ax4.voxels(filled, facecolors='cyan', edgecolor='k', alpha=0.5)

# 在每个体素中显示值
for i in range(2):
    for j in range(2):
        for k in range(2):
            ax4.text(i + 0.5, j + 0.5, k + 0.5, str(tensor_3d[i, j, k]),
                     color='black', ha='center', va='center')

ax4.set_title("三维张量 (3D Tensor)")
ax4.set_xlabel("X 轴")
ax4.set_ylabel("Y 轴")
ax4.set_zlabel("Z 轴")
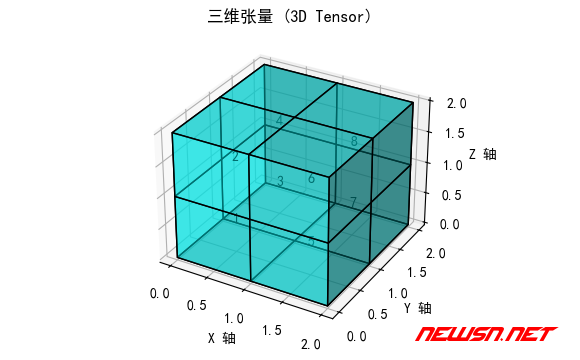
plt.show()

绘制了三维数组 [[[1, 2], [3, 4]], [[5, 6], [7, 8]]] 的体素图。

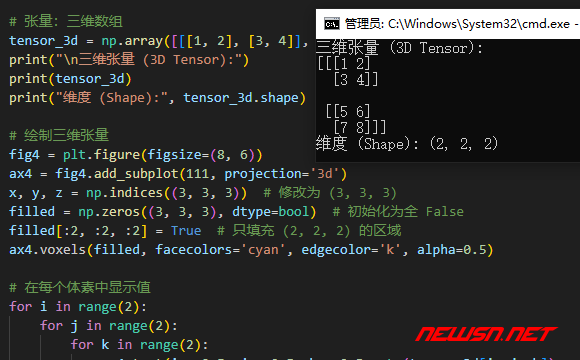
每个小立方体（体素）中标注了对应的值，帮助理解三维张量的结构。

总结

通过上述代码和可视化，我们可以直观地理解标量、向量和张量的区别：

• 标量是单一的数值。
• 向量是一维数组，表示大小和方向。
• 张量是更高维度的数组，可以表示复杂的数据结构。

当然，从二维开始，二维三维都是张量，更高维度也叫张量。但是很难理解了，所以，暂时不在本文的讨论范围内。更多苏南大叔的python相关文章，请参考：

• https://newsn.net/tag/python/

如果本文对您有帮助，或者节约了您的时间，欢迎打赏瓶饮料，建立下友谊关系。
本博客不欢迎：各种镜像采集行为。请尊重原创文章内容，转载请保留作者链接。